For a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees. A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations. Write a function that determines whether two binary trees are flip equivalent. The trees are given by root nodes root1 and root2.
Example 1:
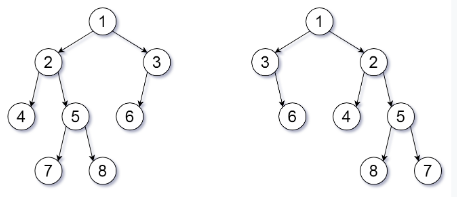
Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
Output: true
Explanation: We flipped at nodes with values 1, 3, and 5.
Flipped Trees Diagram
Note:
- Each tree will have at most 100 nodes.
- Each value in each tree will be a unique integer in the range [0, 99].
Solution in C++
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int ChildSum(TreeNode *node) {
if (!node) return 0;
int sum=0;
if (node->left) sum += node->left->val;
if (node->right) sum += node->right->val;
return sum;
}
int ChildVal(TreeNode *node) {
if (node) return node->val;
return 0;
}
bool flipEquiv(TreeNode* root1, TreeNode* root2) {
if (!root1 && !root2) return true;
if (ChildVal(root1) != ChildVal(root2)) return false;
if (ChildSum(root1)!=ChildSum(root2)) return false;
if (root1->left) {
if (root2->left && ChildVal(root1->left)==ChildVal(root2->left))
return flipEquiv(root1->left, root2->left) && flipEquiv(root1->right, root2->right);
else
return flipEquiv(root1->left, root2->right) && flipEquiv(root1->right, root2->left);
}
else if (root1->right) {
if (root2->right && ChildVal(root1->right)==ChildVal(root2->right))
return flipEquiv(root1->right, root2->right) && flipEquiv(root1->left, root2->left);
else
return flipEquiv(root1->right, root2->left) && flipEquiv(root1->left, root2->right);
}
return true;
}
};
Solution in Java based on Recursion
class Solution(object):
def flipEquiv(self, root1, root2):
if root1 is root2:
return True
if not root1 or not root2 or root1.val != root2.val:
return False
return (self.flipEquiv(root1.left, root2.left) and
self.flipEquiv(root1.right, root2.right) or
self.flipEquiv(root1.left, root2.right) and
self.flipEquiv(root1.right, root2.left))
Solution in Python based on Recursion
class Solution(object):
def flipEquiv(self, root1, root2):
if root1 is root2:
return True
if not root1 or not root2 or root1.val != root2.val:
return False
return (self.flipEquiv(root1.left, root2.left) and
self.flipEquiv(root1.right, root2.right) or
self.flipEquiv(root1.left, root2.right) and
self.flipEquiv(root1.right, root2.left))
Solution in Java based on Canonical Traversal
class Solution {
public boolean flipEquiv(TreeNode root1, TreeNode root2) {
List<Integer> vals1 = new ArrayList();
List<Integer> vals2 = new ArrayList();
dfs(root1, vals1);
dfs(root2, vals2);
return vals1.equals(vals2);
}
public void dfs(TreeNode node, List<Integer> vals) {
if (node != null) {
vals.add(node.val);
int L = node.left != null ? node.left.val : -1;
int R = node.right != null ? node.right.val : -1;
if (L < R) {
dfs(node.left, vals);
dfs(node.right, vals);
} else {
dfs(node.right, vals);
dfs(node.left, vals);
}
vals.add(null);
}
}
}
Solution in Python based on Canonical Traversal
class Solution:
def flipEquiv(self, root1, root2):
def dfs(node):
if node:
yield node.val
L = node.left.val if node.left else -1
R = node.right.val if node.right else -1
if L < R:
yield from dfs(node.left)
yield from dfs(node.right)
else:
yield from dfs(node.right)
yield from dfs(node.left)
yield '#'
return all(x == y for x, y in itertools.zip_longest(
dfs(root1), dfs(root2)))